
Describing motion
Speed and Velocity
Speed – The speed of an object is defined as the change in distance per unit time.
Speed = Total Distance ÷ Total Time
The unit for speed is m/s
Imagine you walked from point A to B which is 500 m away, and then returned back to A, and it took you 2000 seconds.
You walked a total of 1000m in 2000 seconds and therefore your speed was 1000/2000= 0.50m/s.
Sometimes light gates – which emit infrared radiation and are connected to electronic timers – are used to measure accurate timings.
Velocity – Speed is a scalar quantity (magnitude only) whereas velocity is a vector quantity (magnitude and direction)
The concept of velocity is basically speed with a direction. The definition of velocity is the rate of change in displacement.
Displacement is also a vector quantity which is defined as distance traveled in a particular direction.
Velocity = Displacement ÷ Time
Going back to the example above, the total return distance between A & B is 1000 meters.
However, the direction of travel from A to B is the complete opposite of B to A and therefore they actually cancel each other out when we think in terms of displacement.
In other words, your starting point was A and your ending point was also A. Therefore, in that sense, you haven’t actually moved from your original starting point A, and therefore your displacement is actually zero. This means that the velocity will also be 0 as a result (since 0/2000 = 0).
Distance-time graphs – Plots distance traveled versus time.
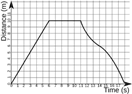
The speed of travel (of any particular section of the graph) can be calculated via the gradient.
A gradient is calculated by using this formula:
Gradient = Change in Y axis ÷ Change in X axis
For example, lets calculate the speed of travel between 0 to 6 seconds on the distance-time graph above.
- The change in X axis = 10m
- The change in Y axis = 6s
- Gradient (speed) = 10/6 = 1.67 m/s
Acceleration
Acceleration – Change in velocity per unit time, and since velocity is a vector quantity, so is acceleration.
(deceleration is just when an object reduces its acceleration, so deceleration is still acceleration)
Acceleration = Change in Velocity ÷ Time Taken
The unit for acceleration is m/s2
Using the formula above, acceleration can be positive or negative
- Acceleration is positive when an object increases in velocity over time. This is what is generally implied when we state that an object is ‘accelerating’.
- Acceleration is negative when an object decreases in velocity over time. We call this ‘deceleration’.
Speed-time graphs – Plots speed against time.
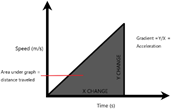
The distance traveled can be calculated via the area underneath the graph and the acceleration can be calculated by the gradient. Here we demonstrate the appearance of this graph under various conditions:

