---

Number

1.1 – Number Facts and Sequences

• Natural Numbers:
• Used for counting purposes
• Made up of all irrational and rational numbers

• Integer: A whole number

• Prime Numbers:
• Only divisible by itself and 1
• 1 is NOT a prime number

• Rational Numbers: Can be written as a fraction
• Irrational Numbers: Cannot be written as a fraction

                                      E.g. π

• Common Factors: Common divisors of a number
• Common Multiples: Multiples of two or more numbers that are the same

• Sequences:
• Finding the nth term:
• Linear Sequence / Arithmetic Sequence:
• Formula to find nth term : a+(n – 1)d
• a = first number in the sequence
• d = difference

E.g.  1,  4 , 7 , 10 , 13

a = 1

d = 3 (4 – 1 = 3, 7 – 4 = 3 etc.)

a+(n – 1)d

= 1 + (n – 1) 3

= 3n – 3 + 1

= 3n – 2              Expression for the nth term

1.2 – Fractions and Decimals

• Converting Fractions to Decimals:
• Divide the numerator by the denominator
• E.g.  7/8  to a decimal

                     7÷8 = 0.875

• Converting Decimals to a Fraction:
• Write down the decimal divided by 1
• E.g.  0.35/1

• Multiply both the numerator and the denominator by 10 for every number after the decimal point
• E.g. 0.35/1           35/100

• Simplify the Fraction
• E.g. 35/100           7/20

            1.3 – Approximations and Estimations

• Rounding Decimals to the Nearest Whole Number:
• If the number after the decimal is less than 5 then round the number down by removing the decimal part of the number
• E.g.  7.3176           7

              This figure is ‘less than 5’

• If the number after the decimal is 5 or more then round the number up by adding 1 on to the ones digit and removing the decimal part of the number.
• E.g.  7.8176           8

                            This figure is ‘5 or more’

• Rounding Decimals to Two/Three Significant Figures:
• Count from the first non–zero digit for two/three digits (0 is not counted as a digit)
• Then round the last digit
• E.g.
• 7.8176            7.82 (3 s.f)

                                        This figure is ‘5 or more’

• 0.078176           0.0782 (3 s.f)

                                              7 is the first significant figure

• Rounding to Two/Three Decimal Places:
• Count from the first digit for two/three digits (0 is counted as a digit)
• Then round the last digit
• E.g. 7.8176            7.818 ( 3 decimal places)

                   This figure is ‘5 or more’

• Measurements and Bounds:
• The ‘unit’ is 1 so ‘half a unit’ is 0.5  (+ 0.5 or – 0.5)           upper bound , lower bound
• The ‘unit’ is 0.1 so ‘half a unit’ is 0.05  (+ 0.05 or – 0.05)           upper bound , lower bound
• The ‘unit’ is 0.001 so ‘half a unit’ is 0.0005  (+ 0.0005 or – 0.0005)           upper bound , lower bound
• E.g.  A length is measured 135 cm to the nearest cm

        The actual length could be anything from 134.5 cm to 135.49999…cm using the normal convention

        which is to round up a figure of 5 or more. Clearly 135.49999… is effectively 135.5 and we say the

        upper bound is 135.5. The lower bound is 134.5

        As an inequality we can write 134.5 ≤ length < 135.5

1.4 – Standard Form

• The number a×10^n is in standard form when 1 ≤ a < 10 and n is a positive or negative integer

10⁴ = 10000	10^ -1 = 0.1
10³ = 1000	10^ -2 = 0.01
10² = 100	10^ -3 = 0.001
10¹ = 10	10^ -4 = 0.0001
10⁰ = 1	10^ -5 = 0.00001

• E.g.
• 2000           2 × 10³
• 150           1.5 × 10²
• 0.0004           4 × 10^ -4

1.5 – Ratio and Proportion

• Ratio:
• Used to describe a fraction
• E.g. 4:7

• Changing to the Form 1:n:
• E.g.  2:5

        2:5 = 1: 5/2

              = 1: 2.5

• Changing to the Form n:1:
• E.g.  2:5

       2:5 = 2/5 :1

              = 0.4:1

• Foreign Exchange:
• Money changed from one currency to another using proportion
• E.g.
• Covert $22.50 to dinars

   $1 = 0.30 dinars (KWD)

   $22.50 = 0.30 × 22.50

               = 6.75 KWD

• Map Scales: Using proportion to work out map scales
• Metric Equivalents:
• 1 km = 1000 m
• 1 m = 100 cm
• 1 cm = 10 mm

1.6 – Percentages

• Converting Percentages to a Fraction:
• Write down the percent divided by 100
• E.g.  35%           35/100

• If the percent is not a whole number, then multiply both top and bottom by 10 for every number after the decimal point
• E.g.  0.35%          0.35/100          35/10000

• Simplify the fraction
• E.g.  35/100          7/20

• Converting Fractions to a Percentage:
• Convert the fraction to a decimal
• Divide the numerator by the denominator
• E.g. ¼  to a decimal

                     1 ÷ 4 = 0.25

•  Multiply by 100 to get percent value
• E.g. 0.25 × 100 = 25

       25%

• Converting Percentages to a Decimal:
• Divide the number (in percentage format) by 100
• E.g. 25% to a decimal

       25/100 = 0.25

• Percentage Increase or Decrease:

• Simple Interest:
• A sum of money $P is invested for T years at R% interest per year the interest gained is given by:

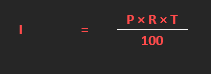
• Compound Interest:
• Formula:

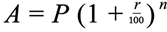
1.7 – Speed, Distance and Time

• Distance = Speed × Time

• Speed = Distance/Time

• Time = Distance/Speed

• Units of Speed:
• km/hr  –  Kilometers per hour
• m/s  –  Meters per second

• Units of Distance:
• km  –  Kilometers
• m  –  Meters

• Units of Time:
• hr  –  Hours
• sec  –  Seconds