
Geometry
4.1 – Fundamental Results
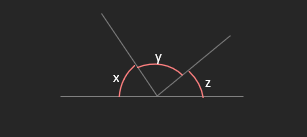
o Angles on a straight line add up to 180°
x + y + z = 180°
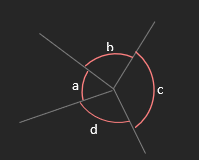
o Angles at a point add up to 360°
a + b + c + d = 360°
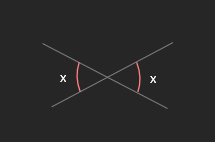
o Vertically opposite angles are equal
x = x
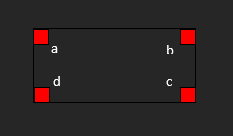
o The sum of all angles in a quadrilateral is 360°
a + b + c + d = 360°
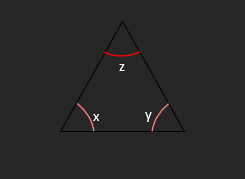
o The sum of all angles in a triangle is 180°
x + y + z = 180°
o An isosceles triangle has 2 sides and 2 angles the same

o An equilateral triangle has 3 sides and 3 angles the same

• Polygons:
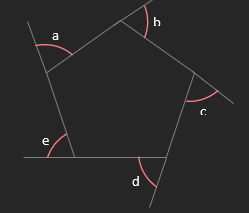
o The exterior angles of a polygon add up to 360°
a + b + c + d + e = 360°
o The sum of interior angles of a polygon = (n – 2) × 180
n = number of sides of the polygon

o A regular polygon has equal angles and sides
• Parallel Lines:
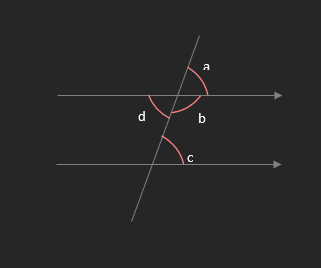
o Corresponding angles are equal
a = c
o Alternate angles are equal
c = d
o Allied angles add up to 180°
b + c = 180°
4.2 – Pythagoras’ Theorem
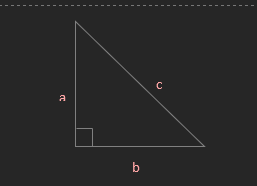
o a² + b² = c²
4.3 – Symmetry
• Line Symmetry:
o A line of symmetry divides a 2D shape into 2 identical shapes.
E.g. The letter A has one line of symmetry

• Rotational Symmetry:
o The order of rotational symmetry is the number of times a shape
fits its outline during a complete rotation
• Quadrilaterals:
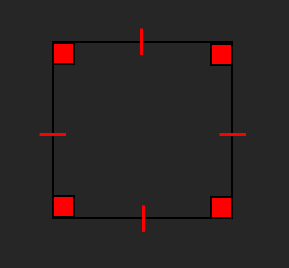
o Square:
All sides are equal
All angles are 90°
Opposite sides are parallel
Diagonals bisect at right angles
4 lines of symmetry
Order of rotational symmetry is 4
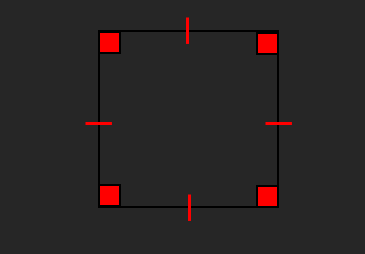
o Rectangle:
Opposite sides are parallel and equal
All angles are 90°
Diagonals bisect each other
2 lines of symmetry
Order of rotational symmetry is 2
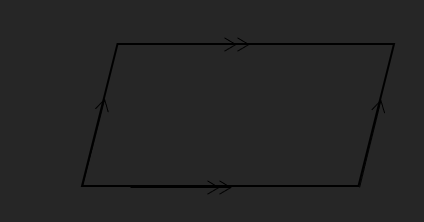
o Parallelogram:
Opposite sides are parallel and equal
Opposite angles are equal
Diagonals bisect each other
No lines of symmetry
Order of rotational symmetry is 2
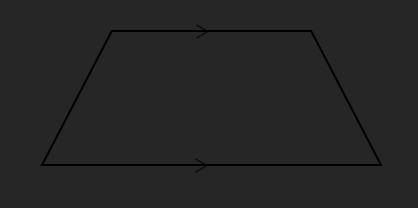
o Trapezium:
One pair of sides are parallel
No lines of symmetry
No rotational symmetry
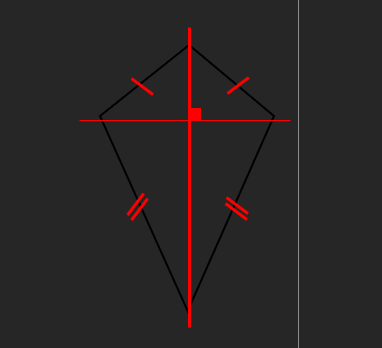
o Kite:
Two pairs of adjacent sides equal
Diagonals meet at right angles bisecting one of them
1 line of symmetry
No rotational symmetry
• Planes of Symmetry:
o A plane of symmetry divides a 3D shape into 2 identical solid shapes.
4.4 – Similarity
o When two shapes’ corresponding sides are proportional
and their corresponding angles equal.
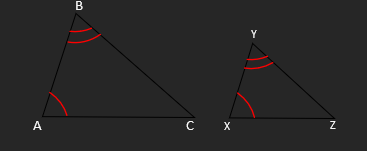
o Two triangles are similar if they have the same angles.
E.g. In triangles ABC and XYZ
A = X and B = Y
∴ The triangles are similar
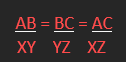
4.5 – Congruence
o When two shapes have exactly the same angles and dimensions.
o To prove that two triangles are congruent, one of the following criteria must be proven:
SSS (Side Side Side): All three pairs of corresponding sides are equal.
ASA (Angle Side Angle): Two pairs of corresponding angles are equal, along with one pair of corresponding sides.
SAS (Side Angle Side): Two pairs of corresponding sides are equal, along with the corresponding angles.
4.6 – Circle Theorems
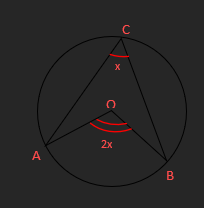
- The angle subtended at the center of a circle is twice the
angle subtended at the circumference.
AÔB = 2 × AĈB
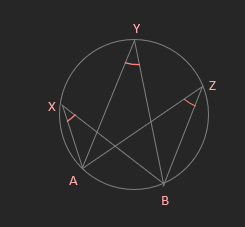
- Angles subtended by an arc in the same segment of a circle
are equal
AXB = AŶB = AZB
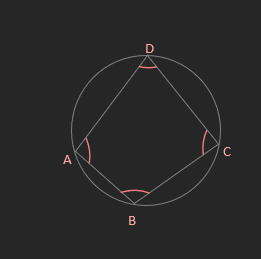
- The opposite angles in a cyclic quadrilateral add up to 180°
A + C = 180°
B + D = 180°
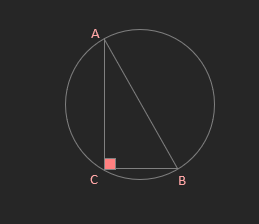
- The angle in a semicircle is a right angle.
AĈB = 90°
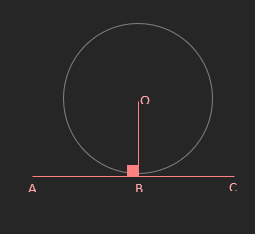
• Tangents to Circles:
- The angle between a tangent and a radius drawn to
the point of contact is 90°
ABO = 90°
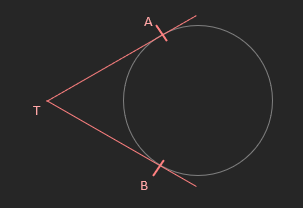
- From any point outside a circle just two tangents
to the circle may be drawn and they are of equal
length.
TA = TB
• The Alternate Segment Theorem:
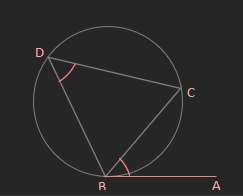
o The angle between a tangent and its cord is equal
to the angle in the alternate segment.
ABC = BDC
4.7 – Constructions
o When constructing, the diagram should be drawn using equipment
such as a pair of compasses and a ruler.
o Constructing Triangles:
Draw the longest side as the base line of the triangle
Set a pair of compasses to one of other lengths given for a side
and draw an arc centered on one end of the base, above the base line.
Similarly, set a pair of compasses to the last length given for a side
and draw an arc centered on the other end of the base, above the base line.
Join this crossing point to each end of the base line.
The triangle has been constructed.
