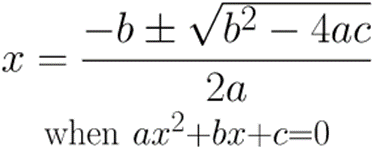---

Algebra 1

2.1 – Brackets and Simplifying

• A term outside a bracket multiplies each of the terms inside the bracket. This is the distributive law
• E.g.  3(x-2y) = 3x – 6y

• ‘Like’ terms can be added:
• x’s cab be added to x’s
• y’s can be added to y’s
• x²’s can be added to x²’s
• E.g.  4x + 3y + 3x² + 4y – x = 3x +7y +3x²

2.2 – Linear Equations

• If the x term is negative, add an x term with a positive coefficient to both sides of the equation
• E.g.  8 – 6x = 4

                8 = 4 + 6x

          8 – 4 = 6x

                4 = 6x

             4/6 = x

             2/3 = x

• If there are x terms on both sides, collect them on one side
• E.g.  4x – 8 = 6 – 6x

        4x + 6x = 6+8

              10x = 14

                  x = 14/10

                  x = 1.4

• If there is a fraction in the x term, multiply out to simplify the equation
• E.g.  4x/6 = 20

            4x = 20 × 6

            4x = 120

              x = 120/4

              x = 30

2.3 – Simultaneous Equations

• Substitution Method: Used when one equation contains a unit quantity of one of the unknowns
• Obtain an equation in one unknown and solve this equation
• Substitute the results from ‘1.’  into the linear equation to find the other unknown
• E.g.  3x – 2y = 0   …[1]

                       2x + y = 7    …[2]

                       2x + y = 7        …[2]

                               y = 7 – 2x

                       Substituting into [1]

                       3x – 2 (7 – 2x) = 0

                          3x – 14 + 4x = 0

                                          7x = 14

                                            x = 14/7

                                            x = 2

                       Substituting into [2]

                       2 × 2 + y = 7

                             4 + y = 7

                                   y = 7 – 4

                                   y = 3

                       The solutions are x = 2, y = 3

• Elimination Method:
• Choose an unknown in one of the equations and multiply the equations by a factor or factors so that this unknown has the same coefficient in both equation

• Eliminate this unknown from the two equations by adding or subtracting them, then solve for the remaining unknown

• Substitute into the first equation and solve for the eliminated unknown

• E.g.  x + 2y = 8   …[1]

        2x + 3y = 14   …[2]

       x + 2y = 8 (×2)   …[1]

        2x + 4y = 16   …[3]

        2x + 3y = 14   …[2]

        Subtract [2] from [3]

         y = 2

                                               Substituting into [1]

                                                x + 2 × 2 = 8

                                                      x + 4 = 8

                                                            x = 8 – 4

                                                            x = 4

                                                The solutions are x = 4, y = 2

2.4 – Factorising

• Common Factors:
• E.g.  6x² + 12x

        6x (x + 2)

• Difference of Two Squares:
• E.g.  49 – x²

        (7 + x) (7 – x)

• Group Factorization:
• E.g.  2b + ac + ab + 2c

         2 (b + c) + a (c + b)

                                       (2 + a)(c + b)

• Quadratic Expressions:
• E.g.  x² + 14x + 24
• Find two numbers which multiply to give 24 and add up to 14
• Numbers are 12 and 2
• Put these numbers into brackets

  x² + 12x + 2x +24

  x (x + 12) + 2 (x + 12)

  (x + 2)(x + 12)

• So x² + 14x + 24 = (x + 2)(x + 12)

2.5 – Quadratic Equations

• Solution by Factors:
• E.g.  x² + 14x + 24 = 0
• Find two numbers which multiply to give 24 and add up to 14
• Numbers are 12 and 2
• Put these numbers into brackets

  x² + 12x + 2x +24 = 0

  x (x + 12) + 2 (x + 12) = 0

  (x + 2)(x + 12) = 0

• Either    x + 2 = 0      or      x + 12 = 0

             x = -2                      x = -12

• Solution by Formula:
• Formula: