---

Decimal and Hexadecimal

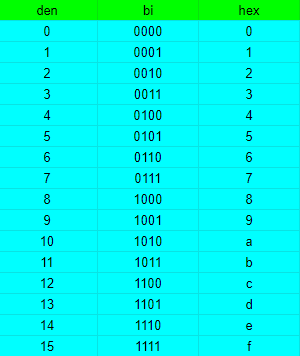
Binary system:

In mathematics and digital electronics, a binary number is a number expressed in the base-2 numeral system or binary numeral system, which uses only two symbols: typically “0” (zero) and “1” (one). Each digit is called a bit.

Its used as a computing language and is also called machine language because this is the only language understood by computers

Binary to Denary: 1. Create table with headings 128/64/32/16/8/4/2/1.

2. Insert the binary number into the table.

3. Add up all numbers that correspond with a 1.

Denary to Binary:

1. Create the same table.

2. Place 1s in the columns that add up to make the denary number.

3. Take the empty spaces as 0 and form a binary number.

Hexadecimal

The hexadecimal numeral system, often shortened to “hex“, is a numeral system made up of 16 symbols (base 16). 

Hexadecimal to Denary:

1. Create table with headings 4096/256/16/1 in the style shown above.

2. Put hex number in columns from right to left.

3. Multiply each hex digit with the corresponding column.

4. Add the values.

E.x: CF8=12,15,8

4096/256/16/1

     12/15/8

12*256 + 15*16 + 8*1 = 3208

Binary to Hexadecimal:

1. Split the binary number into three groups starting from the right.

2. Put each group into a table with 8/4/2/1 columns.

3. Add the columns that correspond with a 1 for each table.

4. Convert all the values into hex format and put them together.


E.x: 101111100001 = 1011, 1110, 0001

8/4/2/1  8/4/2/1  8/4/2/1

1/0/1/1  1/1/1/0  0/0/0/1

8+2+1=11, 8+4+2=14, 1=1

11=B, 14=E

101111100001=BE1

Binary=Base 2

Denary=Base 10

Hexadecimal=Base 16

Every hex number after 9 is a letter.

E.x: A=10, B=11, C=12, etc.

Uses of hexadecimal:

1. Memory dumps-Printed memory used to trace errors while developing software.

2. HTML (Hyper-Text Markup Language)

3. Media Access Control (MAC) address

4. ASCII (American Standard Code for International Interchange) 5. Assembly and Machine code.