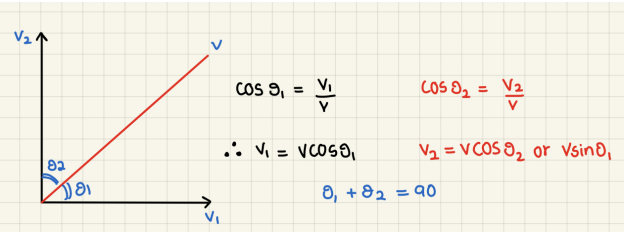---

Vectors

● Quantities that has both magnitude and direction are called vectors
● Eg: force, weight, momentum, acceleration, current
● Quantities that have magnitude (size) only but no direction are called scalers
● Eg: volume, density, distance, pressure, energy, temperature, work


Representing vectors

● Vectors can be represented by arrows in diagrams
● The length of the arrow, represents the magnitude
● The direction of the arrow represent the direction of the vectors


Vectors acting same direction

Resultant = F1 + F2
If 2 vectors acting on the opposite direction

Resultant = F2 – F1 re F1 – F2


Perpendicular vectors

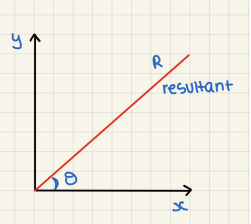
● If two vectors x and y are acting 90 degree to each other, the resultant is the diagonal of the rectangle

● The magnitude of the vector “R” can be found using the pythagoras theorem
R² = X² + Y²

● Direction of the resultant force given by angle “θ”

tan θ = Opposite / adjustment
Tan θ = y / x

Resolving vectors

● We can resolve a vector “v” into two components acting at right angles to each other
● V₁ acts at angle θ₁ to the original vector “v”
● V₂ acts at angle of θ₂ to the original vector