---

Data Types

Built-in Data Types:

• The programming language defines the range of possible values that can be assigned to a variable when its type has been chosen
• The programming language defines the operations available to manipulate values assigned to the variables

User-defined Data Types:

• Programmer includes definition in the program. Once definition is completed, variables can be created with the data type

Non-composite Data Types:

• Defined without reference to another data type
• Examples:
  • Real
  • Integer
  • Boolean 

Enumerated Data Types:

• Example of a user-defined non-composite data type
• Every possible value for the variable is identified during definition
• Values are NOT of type string
• Values are ordered. Due to this property, different variables that are of the enumerated data type can be compared (e.g. one is “larger” than the other). 

Composite Data Types:

• Defined with reference to at least one other built-in data type
• Examples:
  • Record
  • Class
  • Array

Pointer Data Type:

• Variable’s value refers to a memory location

Set Data Types:

• Allows a program to create sets and to apply mathematical operations defined in set theory
• Properties of a set:
  • Contains a collection of data values
  • Values within a set are not organised
  • Duplicated values are not allowed
• Operations that can be performed on a set:
  • Checking for a value
  • Adding a new value
  • Removing an existing value
  • Adding multiple sets together
• Sets are NOT structured, as their values cannot be indexed

16.2: FILE ACCESS

• To store data which is used to input to a computer system or output from one, there are only two defined file types:

1. Text file

• Contains data stored according to a character code (e.g. Unicode)
• For each file, the number of data items per line and the number of characters per item must be known. If not, item separator characters must be used. End-of-line is indicated using a line terminating character

2. Binary file

• Data stored in internal representation
• Organisation based on record concept
• Number of fields per record must be known. If a field contains a string, the length of the string must be known. For any other field, internal representation defines the number of bytes required to store the field value. End-of-field and field separator characters not used.

Serial Files:

• Contain unorganised records
• Example use: a bank recording customer transactions. Each time a new transaction is completed, the transaction details are appended to the file, so the only order is the time at which each transaction took place (i.e. the file is ordered chronologically)

Sequential Files:

• Contains ordered records
• Contains a key field with values that are unique but not always consecutive. This field allows the records to order themselves. 

Direct-Access Files:

• Also referred to as random-access files (any random record in the file can be accessed without the file being read in any order)
• Direct access can be achieved using sequential files. In this case, a separate “index file” is created, which contains two fields per record: one with the key field value and the other with a value which indicates where the key field is located in the main sequential file
• An alternative method of creating a direct access file is to use a hashing algorithm to calculate the address where the record input will be stored. Using this method, it is clear that there is no order which the address calculation follows (i.e. it is not sequential).
• Also, using a hashing algorithm to calculate the address where the record will be stored can produce the same address for two different records. This results in a “collision”, where the two addresses are called “synonyms”. In most cases, the number to divide the record value by is calculated to minimise collisions and spread the records across all records as evenly as possible. However, not all collisions are avoidable, so a method of dealing with collisions must be clearly defined. For example:
  • Searching sequentially for the next available address
  • Accounting for collisions by keeping a number of overflow addresses available for storage
  • Having a linked list from each address available

File Access:

• For a serial file, most data is accessed by reading the file record by record
• For a sequential file, data is accessed the same way. However, if the key field value for the wanted record is known, the process is faster, as only the key field values need to be read through.
• For a direct-access file that uses a hashing algorithm, the value in the key field is passed through the hashing algorithm to obtain the address at which the wanted record is stored. This removes the need for reading the entire file from its beginning. However, to account for collisions, some serial searching might be required after the address value is calculated (i.e. records might need to be read one after the other to find the address). 
• When deleting/editing data in a sequential file, a new file is created. Old records are copied to the new file until the record to be deleted/edited is reached. Once it is reached, the record is edited/deleted as needed and the remaining records are copied to the new file as well. This is the same method used by a sequential file when a record is added to it
• For a direct access file, no reading through the file is required if a record must be edited. The record to be edited is accessed directly and edited as needed. However, if a record is to be deleted, a flag is set on the record, and when the file is read next, that record is skipped.   

Choice of File Organisation:

• Serial files: used for batch processing or backing up data on a magnetic tape 
• Direct-access: used if a single record is needed from a large file (e.g. on a system that many users access. In this case, the file that keeps a track of all the users’ passwords should be direct-access)
• Sequential files: used when multiple records are required from a single file search. For example, in a database at a hospital/clinic, inputting a single data value (e.g. a family name) provides multiple records (e.g. all patients with the same last name)

* A note on primary keys in a database VS key fields in files:

In a database, the values in the primary key must be all unique, whereas in key fields in files, this is not a requirement. Sometimes it is necessary for them to be unique, depending on the purpose of and records in the file, but this is not mandatory.

16.3: REAL NUMBERS

• Fixed point representation: The direct conversion of a denary number to binary using the below scale:
  
  

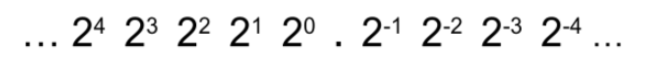
The decimal place is kept in the same position and the integer part of the number is converted to binary. For the decimal part, the number is split into numbers which are equal to 2^-position (see the example below). 

• Floating point representation: the decimal is moved to immediately after the first binary number. The number of places the decimal is shifted becomes the exponent. 

• Denary → floating point conversion:
  

Example: 16.75

Step 1: Fixed point representation

Step 2: Floating point representation:

To move the decimal to immediately after the first number, it must be moved 5 places. So, the exponent becomes 5. In floating point representation, the number is represented as [mantissa] [exponent]. Though the decimal is implied to be after the first number, it is not seen in actual notation. In this case:

010000.11 = 01000011 0101

Note that the mantissa begins with a 0. This signifies that the number is positive. If a number in floating point representation begins with a 1, it is a negative number!

• Floating point → denary:

Example 01010110 0100

Step 1: Fixed point representation:

01010110 0100 = 0.1010110 x 2⁴ 

As the exponent is 4, the decimal must be shifted 4 places to the right, 

giving 01010.110. The trailing 0 from the decimal part and the beginning 0 

from the integer part can be removed, as they are insignificant to the final 

number: 1010.11

Step 2: Binary to denary:

1010.11 is split into 1010 and .11

1010 = 12

.11 = 0.50 + 0.25

      = 0.75

∴ 1010.11 = 12.75

∴ 1010110 0011 = 12.75

• To convert negative denary numbers, find the floating point representation equivalent of the positive number and then convert the mantissa to two’s complement. To convert a negative floating point representation to denary, convert the mantissa using two’s complement, solve it normally and then add the ‘-’ to the denary number. 

• Precision and normalisation:
  • Precision: how accurate the binary number is to the intended denary number. This is increased by increasing the number of bits available to represent the mantissa, and maximised by normalising the floating point number (see below). 

• Normalisation: ensuring the floating point representation’s first two numbers are different. To ensure a number is normalised, add/remove 0s as required, and adjust the exponent value (increase/decrease it) accordingly. Examples:

1. 00110011 0100. To normalise this number, the second 0 should be removed. If this is done, the value of the exponent must be reduced by 1 to account for the removal of the 0. So, the normalised version becomes 0110011 0011

2. 11001110 0011. To normalise this number, first convert it to its two’s complement form (-00110010 0011). Then normalise this number using the method in example 1, which gives the result -01100100 0010. Finally, convert the negative number to its two’s complement form to give the final normalized number (10011100 0010)

• An important thing to note is the significance of increasing/decreasing the number of bits available to represent the mantissa/exponent of a number:
  • Increasing the number of bits that represent the mantissa increases the precision of the number being represented, while decreasing the number decreases the precision
  • Increasing the number of bits that represent the exponent increases the range of numbers that can be represented, while decreasing the number decreases the range