Moles and Equations

1.1: MASSES OF ATOMS AND MOLECULES

Relative Atomic, Isotopic, Molecular and Formula Masses:

Relative atomic mass (A_r): the weighted average of naturally occurring isotopes of an element on a scale where an atom of carbon-12 (¹²C) has a weight of exactly 12 units
Relative isotopic mass: the weight of the isotope on a scale where an atom of carbon-12 (¹²C) has a weight of exactly 12 units
Relative molecular mass (M_r): the weight of one molecule of a substance on a scale where an atom of carbon-12 (¹²C) has a weight of exactly 12 units. This can be found by adding up the relative atomic masses of the elements making up the substance in question. For example:

Find the M_r of CuSO₄

A_r of Cu = 63.5

A_r of S = 32.1

A_r of O = 16.0

∴ M_r of CuSO₄ = 63.5 + 32.1 + (4 x 16.0)

= 159.6

When finding the Mr of a compound that does not have all its elements in a 1:1 ratio (e.g. CuSO₄, Ba(OH)₂, H₃PO₄), multiply the A_r of the element which has multiple atoms for every one atom of another element. For example, in the question above, there are four atoms of oxygen for every one atom of copper and every one atom of sulfur. Thus, the A_r of oxygen must be multiplied by 4 and then added to the rest of the values. Similarly, when calculating the M_r of Ba(OH)₂, find the M_r of OH, multiply it by 2 and then add it to the A_r of barium to find the Mr of Ba(OH)₂.

Relative formula mass (M_r): M_r of an ionic compound, calculated the same way the relative molecular mass of a compound is (see above).

Mass Spectrometry:

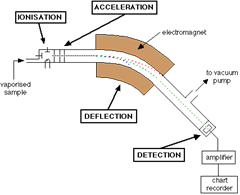
There are four stages to every mass spectrometry procedure:

Ionisation: the sample of gaseous atoms is bombarded with electrons, forming gaseous ions
Acceleration: the gaseous ions are then accelerated along the path they must travel until they arrive at the electromagnetic field
Deflection: once the ions reach the electromagnetic field, they are deflected so that the different isotopes in the sample separate. The degree of separation/deflection is determined by the isotope’s mass:charge (m/e or m/z) ratio. The larger the m/e value, the larger the angle of deflection.
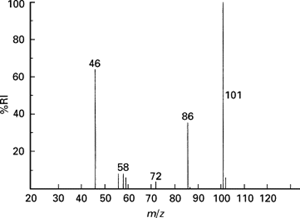
Detection: the different ion isotopes, now deflected, are detected electronically, and the relevant data is displayed in a mass spectrum (shown below).

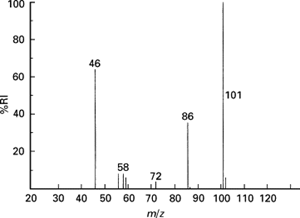
The x-axis shows the relative atomic mass of each isotope (also marked next to each bar) and the y-axis shows the relative abundance of each isotope. The taller the bar, the larger the relative abundance.

1.2: ACCURATE RELATIVE ATOMIC MASSES:

To calculate the relative atomic mass of a sample from a mass spectrum diagram, we need the following:
- The percentage abundance (the height of each peak on the diagram)
- The mass number of the isotope (the position of each bar on the x – axis)
To calculate the sample’s relative atomic mass, multiply the mass number of each isotope with its corresponding percentage abundance, add all the results together and divide the sum by 100. Consider the mass spectrum at the bottom-right corner. To calculate the zirconium sample’s relative atomic mass, following the above steps, we get the following result:

1.3: AMOUNT OF SUBSTANCE

Mole: amount of a substance that has the same number of atoms/molecules/ions as there are atoms in 12g of carbon-12 (¹²C)
- From this definition, we see that 1g of any substance does not mean 1 mole of the same substance. To find out how many moles of a substance there are in a sample, use the following equation:

Molar mass (M): the mass of 1 mole of any substance (g mol^-1)
Avogadro’s number/constant (L/N_A): the number of atoms in 1 mole (6.02 x 10²³). This number also applies to molecules/ions (e.g. there are 6.02 x 10²³ atoms in 1 mole of lithium, and 6.02 x 10²³ molecules in 1 mole of lithium fluoride).

1.4: MOLE CALCULATIONS

You may come across questions where you will be given reactants in an equation, the products formed and the mass of one reactant, and asked to find how much of a product is formed. Consider the below question:

Iron (III) oxide reacts with carbon monoxide to form iron and carbon dioxide. Calculate the mass of iron produced when 798g of iron(III) oxide is reduced by excess carbon monoxide.

Step 1: Write out a balanced equation

Fe₂O₃ + __CO → __Fe + __CO₂

Start by balancing the metal ions involved. Since there are two atoms of Fe on the reactants side, the coefficient of Fe on the products side becomes 2.

Next, try to balance the rest of the elements. In this case, since CO₂ is produced, that means that there needs to be an even number of oxygen atoms on the reactant’s side. There are already four atoms of oxygen on the reactants side (three from Fe2O3, one from CO), meaning the coefficient of CO2 could be 2. This would mean that there are two carbon atoms on the product’s side, and the coefficient of CO would be 2. However, this changes the number of oxygen atoms to a total of 5, which doesn’t work because the number of oxygen atoms would be odd. To solve this problem, increase the coefficient of CO on the reactant’s side to 3. This makes the number of oxygen atoms a total of six (even), and the number of carbon atoms three. Since there are three carbon atoms on the reactants side, the coefficient of CO₂ on the products side becomes 3, causing the number of carbon atoms on the reactants and products side to match (3), and the number of oxygen atoms to match as well (6). This results in the following equation:

Fe₂O₃ + 3CO → 2Fe + 3CO₂

Step 2: Determine the moles of the substance whose mass you have been given

You have been given that 798g of iron(III) oxide is involved in the reaction. To find the moles of iron (III) oxide in 798g, use the following equation:

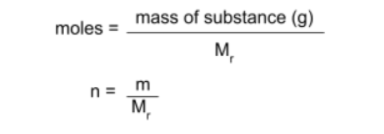
Following the equation and the data we have, we end up with the following result:

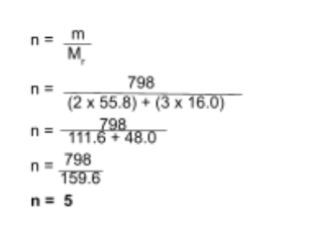
Step 3: Use the ratio of reactant:product to find the moles of the product formed

In general, to find the ratio of reactant:product, you must look at the coefficients of each molecule. In our equation, the coefficient of Fe₂O₃ is 1 and the coefficient of Fe (the product we must find) is 2. This means that the ratio of Fe₂O₃ : Fe is 1:2.

As we found in step 2, the moles of Fe2O3 reacted is five. Using the 1:2 ratio, we find that ten moles of Fe are formed.

Step 4: Find the mass of product formed

The final step is to use the mole equation (n = m/M_r) to find the mass of Fe formed, as seen below:

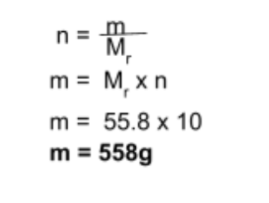
Note: when doing mathematical calculations in chemistry, if the number of significant figures is not mentioned in the question, you are expected to use the same number of significant figures as the least number used in the data given.
Sometimes, you may be asked to find the percentage composition by mass of an element in a compound. Consider the below question:

Find the percentage composition by mass of copper in CuSO₄.

Calculating Empirical and Molecular Formulae:

Empirical formula: the simplest whole number ratio of elements in a compound
Molecular formula: the total number of atoms of each element in a compound
The molecular formulae for all ionic compounds are the same as the empirical formulae, while the molecular formulae for most organic compounds are different from their empirical formulae
Given the molecular mass of a compound, to find its empirical formula, simply divide the atom numbers by their highest common factor (e.g. to find the empirical formula of N₂H₄, divide the atom numbers (2 and 4) by their highest common factor (2) to arrive at the answer: NH₂).
You may come across questions which give you the percentage composition by mass of elements in a compound and ask you to find the empirical formula of the compound. Consider the below question:

A compound X is composed of 6.21g of Pb and 0.72g of O. Find its empirical formula.

Step 1: Find the moles of each element in the compound

Use the mole equation to find the moles of each element:

Step 2: Find the simplest whole number ratio

Divide the calculated mole quantities by the smallest value to find the simplest

whole number ratio:

You may also be asked to find the molecular formula of the compound, given the compound’s relative molecular mass. Consider the below question:

The relative molecular mass of compound X, now found to be Pb₂O₃, is 462g. Find the compound’s molecular formula.

Use the formula MF = x(EF), where x is the ratio of the molecular formula’s mass to the empirical formula’s mass:

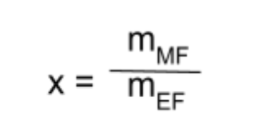
The molecular formula’s mass will always be greater than or equal to the mass of the empirical formula. In this case, the mass of the sample is 462g, which is the same as the empirical formula’s mass. This means, following the formula above, x = 1. From this, we see that in this case, the molecular formula is the same as the empirical formula (Pb₂O₃).

1.5: CHEMICAL FORMULAE AND EQUATIONS

To deduce the formula of an ionic compound, simply write the metal ion, the charge of the non-metal ion as the subscript, the non-metal ion, and the charge of the metal ion ast the subscript. Examples:

Compound ions: ions w/ multiple elements in them (e.g. SO₄^2-, CO₃^2-, PO₄^3-). The same principle above applies to them too.
For simple covalent compounds, their symbols are drawn up according to how many electrons the central ion needs to enter the octet state. For example in methane (CH₄), the central carbon ion needs four electrons to enter the octet state and become stable. Hence, four H⁺ ions are needed to stabilize the central carbon ion.
Naming:
- metal + non-metal = metal non-metal-ide (e.g. sodium + fluorine = sodium fluoride)
- Compound ion w/ oxygen: non-metal-ate (e.g: NO₃^2- = nitrate, SO₄^2- = sulphate)

State Symbols:

It is good practice to write out equations using the state symbols to indicate the state of matter in which the substance referred to is. The following are the different state symbols you can use:
- (s) = solid
- (l) = liquid
- (g) = gas
- (aq) = aqueous (dissolved in H₂O)
Example: CaCO_3(s) + 2HCl_(aq) → CaCl_2(aq) + CO_2(g) + H₂O_(l)

Ionic Equations:

Spectator ions: those that do not take part in a reaction happening in a solution
Ionic equations: shows only ions that are reacting and ∴ are simpler than full equations
- Steps:
Write out the full balanced equation
Write all the ions present. If a reactant or product has the state symbol (s), (l) or (g), or is a molecule dissolved in H₂O (i.e. aqueous), it does not split into ions
Cancel the spectator ions (they will appear on both sides of the equation
Write out the ionic equation left

Example: write the ionic equation for the reaction between aqueous Cl₂ and aqueous KBr.

Step 1: Cl_2(g) + 2KBr_(aq) → 2KCl_(aq) + Br_2(aq)

Step 3: Cl_2(g) + ~~2K+_(aq)~~ + 2Br-_(aq) → ~~2K+_(aq)~~ + 2Cl-(aq) + Br_2(aq)

Step 4: Cl_2(g) + 2Br-_(aq) → Br_2(aq)+ 2Cl-(aq)

For a precipitation reaction, writing an ionic equation is easier. Simply:
Write the precipitate formed as the product
Write the ions that make the precipitate as the reactant

Example: write the ionic equation for the reaction of CuCl_2(aq) with K₂SO_4(aq).

In this case, the full balanced equation is:

CuCl_2(aq) + K₂SO_4(aq) → CuSO_4(s) + 2KCl_(aq)

Step 1: We know this is a precipitation reaction, so the precipitate formed will be CuSO₄. Thus, this becomes the product.

Step 2: Because we know the precipitate is CuSO₄, we know that the ions forming the precipitate are Cu²⁺ and SO4^2-, which become the reactants

Thus, we write the ionic equation as such:

Cu²⁺ + SO₄^2- → CuSO_4(s)

1.6: SOLUTIONS AND CONCENTRATION

Concentration formula:

Hint: This gives us the second equation we can use to calculate moles (n = cv)! Note that this is used only when finding moles of a liquid in a solution
Since concentration is measured in mol dm^-3, ensure your quantities are in the correct units!

Titrations:

Commonly used for neutralisation reactions
Process:
Get some acid of known concentration (e.g. HCl)
Wash a burette with a little acid, and then fill it up with the same acid.
Record the initial burette reading
Measure a known volume of alkali solution (e.g. NaOH) into a flask using a pipette
Add a few drops of indicator solution (e.g. litmus/phenolphthalein) to the flask
Slowly add the acid from the burette by opening the valve at the bottom, and keep swirling the flask until a colour change is seen (i.e. the end-point)
From this point, add acid drop-by-drop until no further colour change is seen (i.e. all the alkali is reacted)
Record the final reading. The difference between the final and initial readings is the rough titre
Repeat the process until two consecutive titres have a value difference of 0.10 cm³ or less
Take the average of the two values to find the volume of acid needed to neutralize the sample of alkali

Calculating solution concentration by titration:
- To do this, we need to know both the concentration and volume used of one of the reactants

Example:

25.0 cm³ of a solution of sodium hydroxide is exactly neutralised by 15.10 cm³ of sulfuric acid of concentration 0.200 mol dm^-3.

2NaOH + H₂SO₄ → Na₂SO₄ + 2H₂O

Calculate the concentration, in mol dm^-3, of the sodium hydroxide solution.

Step 1: Find the moles of H₂SO₄

Use the mole equation (n = cv) to find the moles of H₂SO₄ used to neutralize the NaOH sample.

Step 2: Use the stoichiometric ratios to find the moles of NaOH reacted

Step 3: Find the concentration of NaOH in the sample

Use the mole equation n = cv to find the concentration of the NaOH sample.

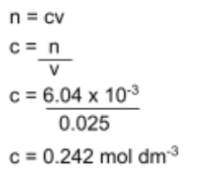
Deducing stoichiometry by titration:
- To do this, we need to know the concentrations and volumes of both reactants

Example:

25.0 cm³ of a 0.0500 mol dm^-3 solution of lithium hydroxide was titrated against a solution of 0.200 mol dm^-3 hydrochloric acid. It required 12.50 cm³ of hydrochloric acid to exactly neutralise the lithium hydroxide. Deduce the stoichiometry of this reaction.

Step 1: Calculate the moles of both reagents

Use the moles equation n = cv to find the moles of both reagents.

Step 2: Find the stoichiometric ratio between the two reactants

To complete this step, divide both values of n by the smallest n value

Therefore, you have the final equation, LiOH + 2HCl → LiCl + H₂O.

1.7: CALCULATIONS INVOLVING GAS VOLUMES

There is one final mole equation that you can use for questions specifically involving gases:

In the above equation, the value 24 is known as the molar gas volume, which was hypothesized by Avogadro to be the volume of space occupied by one mole of any gas at room temperature and pressure.
We can use the above equation to find the ratio of reacting volumes of gases in an equation, which can be used to find out the stoichiometry of an equation.

Example:

50 cm³ of a gaseous hydride of phosphorus, PH_n reacts with exactly 150cm³ of chlorine, Cl₂, to form liquid phosphorus trichloride and 150cm³ of hydrogen chloride gas, HCl.

Deduce the formula of the phosphorus hydride (PH_n) and thus the full equation.

Step 1: Find the stoichiometric ratios between the substances

From the question, we already have a rough outline of the full equation, as well as the volumes of some of the substances involved:

__PH_n + __Cl₂ → __PCl₃ + __HCl

(50 cm³) (150 cm³) (150 cm³)

We can use the mole equation we just learned, as the reactants involved are gaseous:

This gives us the coefficients for some of the substances in the equation:

PH_n + 3Cl₂ → __PCl₃ + 3HCl

Since the coefficient of HCl is 3, this means there are 3 atoms of hydrogen on the products side. Further, since the only molecule that has hydrogen in it in the reactants side is the phosphorus hydride, it follows that the value of n is 3, thus giving us the formula of the hydride: PH₃. Lastly, since the coefficient of PH₃ is 1, and the only molecule on the products side that has phosphorus in it is PCl₃, it follows that the coefficient of PCl₃ becomes 1. Thus, we have the final full equation:

PH₃ + 3Cl₂ → PCl₃ + 3HCl