---

5.  Algebra 2

         5.1 – Algebraic Fractions

• Simplifying Fractions:

• Can simplify algebraic fractions using division
• Where possible factorise the numerator and denominator, then cancel common factors.
• E.g.     5x² – 245      

• Addition and Subtraction of Algebraic Fractions:

• To add or subtract algebraic fractions:

1. Find the lowest common multiple of the denominators
2. Express fractions in terms of the L.C.M
3. Simplify numerators 
4. Add numerators

• E.g.  5x  +  2x     (Lowest common denominator of 6 and 9 is 18)

5.2 – Changing the Subject of a Formula

• When changing the subject of a formula, you rearrange it so that you have a different subject
• To do this, move a term from one side of the equal sign to the other side and change the operation to do the opposite (inverse operation).

• E.g. Make ‘y’ the subject of the formula x(y – z) = a

       x(y – z) = a

       xy – xz = a

               xy = a + xz

                 y = a + xz

                           x

 5.3 – Variation

• Direct Variation:

• Several ways of expressing a relationship between two quantities ‘x’ and ‘y’
• E.g.  

• ‘x’ varies directly as ‘y’
• ‘x’ varies as ‘y’
• ‘x’ is proportional to ‘y’

• These all mean the same and can be written in symbols:
• x ∝ y

• ‘∝’ sign can be replaced with ‘= k’ where k is a constant:
• x = ky

• E.g.  Suppose x = 6  when y = 24

          6 = k × 24

          k = 6/24

          k = ¼

You can then write x = ¼ × y, this enables you to find any value of ‘x’ for any value of ‘y’ and vice versa.

• Inverse Variation:

• Several ways of expressing an inverse relationship between two variable ‘x’ and ‘y’
• E.g.

• ‘x’ is inversely proportional to ‘y’
• ‘x’ varies inversely as ‘y’

• These all mean the same and can be written in symbols:
• x ∝ 1/y

• ‘∝’ sign can be replaced with ‘= k’ where k is a constant:
• x = k × 1/y

              5.4 – Indices

• Rules of Indices:

1. aⁿ × a^m = a^{n + m}

• E.g. 4² × 4⁴ = 4⁶

2. aⁿ ÷ a^m = a^{n – m} 

• E.g. 3⁵ ÷ 3² = 3³

3. (aⁿ)^m = a^{n m}

• E.g. (2⁴)⁵ = 2²⁰

4. a^-n = 1/aⁿ 

• E.g. 6^-2 = 1/6²

5. a^1/n  means the nth root of a

• E.g. 8^1/2 = √8

6. a^m/n  means the nth root of a raised to the power m

• E.g. 5^3/2 = (√5 )³

              5.5 – Inequalities

• < (less than)

• E.g.  x < 5  (x is less than 5)

• > (greater than) 

• E.g.  x > 8  (x is greater than 8)

• ≤ (less than or equal to) 

• E.g.  x ≤ 12  (x is less than or equal to 12)

• ≥ (greater than or equal to) 

• E.g.  x ≥ 4  (x is greater than or equal to 4)

• Solving Inequalities:

• You use the same procedure used for solving equations.
• Except when you multiply or divide by a negative number the inequality will be reversed

• E.g.  12 – 3x < 27

                                                      -3x < 15   (Subtract 12 from both sides)

                                                          x > -5   (Divide both sides by -3)

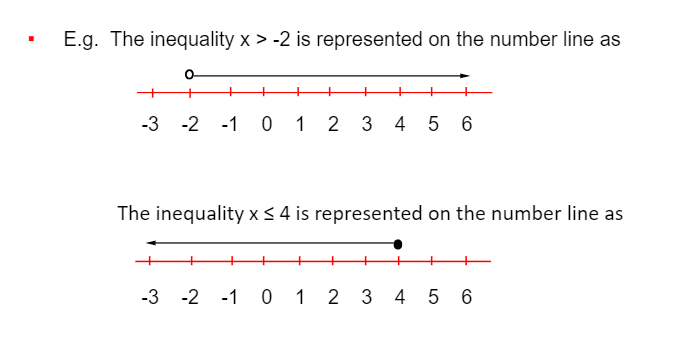
• The Number Line:

• You may need to represent inequalities on a number line.

• is used for < and > and means the end value is not included
• is used for ≤ and ≥ and means the end value is included 

                 5.6 – Linear Programming

• In most linear programming problems, there will be two stages:

1. Interpret the information given as a series of simultaneous inequalities and display them graphically.

Investigate some characteristic of the points in the unshaded solution set.